Arreglos
Acontinuacion se abarcara toda la informacionde de arreglos asi como sus tipos y ejemplos graficos de como se representan
Definicion
Un arreglo (vector, array, matriz) es un conjunto de datos o una estructura de datos homogéneos que se encuentran ubicados en forma consecutiva en la memoria RAM (sirve para almacenar datos en forma temporal).
Es un conjunto de datos que se almacenan en memoria de manera contigua con el mismo nombre. Para diferenciar los elementos de un arreglo se utilizan índices detrás del nombre del arreglo y encerrados por []. El elemento 5° (quinto) de un arreglo, es representado por el índice [4], ya que los índices comienzan en 0. Esto significa que un arreglo de 10 elementos tendría los índice del 0 al 9: [0...9]
Un arreglo es un grupo de ubicaciones de memoria consecutivos, todas ellas del mismo tipo. Para hacer referencia a una ubicación o elemento especifico en el arreglo, específicamente su nombre y el número de posición del elemento especifico en el arreglo.
El número de posición se le conoce como el índice o subíndice, el primer elemento en todo arreglo tiene el subíndice 0 y se conoce algunas veces cono elemento cero.
Tipos de Arreglos
Arreglos unidimensionales
El tipo más simple de arreglo es el arreglo unidimensional o vector. Un vector de una dimensión denominado NOTAS que consta de n elementos. El subíndice o índice de un elemento [1, 2, 3, i…, n] designa su posición en la ordenación del vector. Para hacer referencia a un elemento del vector se usa el nombre del mismo, seguido del índice (entre corchetes), el cual indica una posición en particular del vector.
Aqui un ejemplo de un arreglo unidimensional
supongamos que queremos guardar las notas de los 20 alumnos de una clase. Podemos representar gráficamente el array de notas de la siguiente forma:

Para acceder a cada elemento del array se utiliza el nombre del array y un índice que indica la posición que ocupa el elemento dentro del array. El índice se escribe entre corchetes.
El primer elemento del array ocupa la posición 0, el segundo la posición 1, etc. En un array de N elementos el último ocupará la posición N-1. En el ejemplo anterior, notas[0] contiene la nota del primer alumno y notas[19] contiene la del último. Los índices deben ser enteros no negativos.
Para crear un array se deben realizar dos operaciones: declararlo e instanciarlo. En la declaración se crea la referencia al array. La referencia será el nombre con el que manejaremos el array en el programa. Se debe indicar el nombre del array y el tipo de datos que contendrá.
Arreglos bidimensionales
Los arreglos bidimensionales son aquellos que tienen dos dimensiones y, en consecuencia se manejan con dos índices, se puede ver también como un arreglo de arreglos.
Un arreglo bidimensional equivale a una tabla con múltiples fila y multiiples columnas.
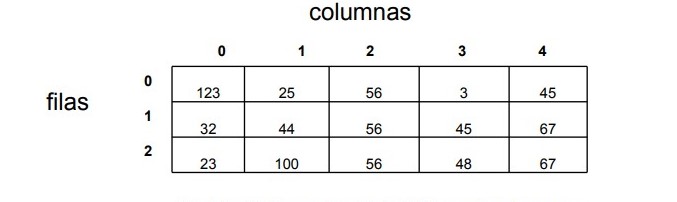
Arreglos multimensionales
Un arreglo se puede definir de tres, cuatro y hasta n dimensiones. Se manejan los mismos conceptos para los subíndices que en los vectores o matrices. Cada elemento del arreglo se puede identificar usando la cantidad de subíndices necesarios, por ejemplo en un arreglo de n dimensiones se escribirá: A [I1, I2, I3,…, In]
Es un tipo de dato estructurado, que está compuesto por dimensiones. Para hacer referencia a cada componente del arreglo es necesario utilizar n índices, uno para cada dimensión. El término dimensión representa el número de índices utilizados para referirse a un elemento particular en el arreglo. Los arreglos de más de una dimensión se llaman arreglos multidimensionales
Los arreglos multidimensionales son una ampliación de las matrices de dos dimensiones y utilizan subíndices adicionales para la indexación. Un arreglo 3D, por ejemplo, utiliza tres subíndices. Los dos primeros son como una matriz, pero la tercera dimensión representa páginas u hojas de elementos

Arreglos con múltiple subíndices
Es la representación de tablas de valores, consistiendo de información arreglada en renglones y columnas. Para identificar un elemento particular de la tabla, deberemos de especificar dos subíndices; el primero identifica el renglón del elemento y el segundo identifica la columna del elemento. A los arreglos que requieren dos subíndices para identificar un elemento en particular 3. se conocen como arreglo de doble subíndice. Note que los arreglos de múltiples subíndices pueden tener más de dos subíndices. El estándar ANSI indica que un sistema ANSI C debe soportar por lo menos 12 subíndices de arreglo.
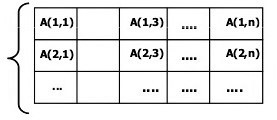
Note que los arreglos de múltiples subíndices pueden tener más de dos subíndices. El estándar ANSI indica que un sistema ANSI C debe soportar por lo menos 12 subíndices de arreglo.
Siguiente tema a profundizar
Le invitamos a acceder al siguiente link donde encontraremos los temas vectores y mattices con todos sus conceptos previos para su conocimiento asi como ejemplos, videos y fotos 👇👇😃.
Vectores y Matrices